MECÂNICA GRACELI - QUÂNTICA TENSORIAL DE CAMPOS [595]

$equação Graceli estatística tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

[

$\psi ^{*}$

$TeoriaInteraçãomediadorMagnitude relativaComportamentoFaixaCromodinâmicaForça nuclear forteGlúon10411/r71,4 × 10-15 mEletrodinâmicaForça eletromagnéticaFóton10391/r2infinitoFlavordinâmicaForça nuclear fracaBósons W e Z10291/r5 até 1/r710-18 mGeometrodinâmicaForça gravitacionalgráviton101/r2infinito$

Teoria	Interação	mediador	Magnitude relativa	Comportamento	Faixa
Cromodinâmica	Força nuclear forte	Glúon	1041	1/r7	1,4 × 10-15 m
Eletrodinâmica	Força eletromagnética	Fóton	1039	1/r2	infinito
Flavordinâmica	Força nuclear fraca	Bósons W e Z	1029	1/r5 até 1/r7	10-18 m
Geometrodinâmica	Força gravitacional	gráviton	10	1/r2	infinito

O produto da incerteza associada ao valor de uma coordenada x_i e a incerteza associada ao seu correspondente momento linear p_i não pode ser inferior, em grandeza, à constante reduzida de Planck.^[6] Em termos matemáticos, exprime-se assim:

$equação Graceli estatística tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

\Delta x_{i}\Delta p_{i}\geq {\frac {\hbar }{2}}

onde $\hbar$ é a Constante de Planck (h) dividida por 2π.

A explicação disso não é fácil de se entender, e fala mesmo em favor da intuição, embora o raciocínio clássico e os aspectos formais da análise matemática tenham levado os cientistas a pensarem diferentemente por muito tempo. Quando se quer encontrar a posição de um elétron, por exemplo, é necessário fazê-lo interagir com algum instrumento de medida, direta ou indiretamente. Por exemplo, faz-se incidir sobre ele algum tipo de radiação. Tanto faz aqui que se considere a radiação do modo clássico - constituída por ondas eletromagnéticas - ou do modo quântico - constituída por fótons. Caso se queira determinar a posição do elétron, é necessário que a radiação tenha comprimento de onda da ordem da incerteza com que se quer determinar a posição.^[7]

Neste caso, quanto menor for o comprimento de onda (maior frequência), maior será a precisão. Contudo, maior será a energia cedida pela radiação (onda ou fóton) em virtude da relação de Planck entre energia e frequência da radiação

$equação Graceli estatística tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

E=h\cdot \nu

e o elétron sofrerá um recuo tanto maior quanto maior for essa energia, em virtude do efeito Compton. Como consequência, a velocidade sofrerá uma alteração não de todo previsível, ao contrário do que afirmaria a mecânica clássica.

Argumentos análogos poderiam ser usados para se demonstrar que, ao medir-se a velocidade com precisão, alterar-se-ia a posição de modo não totalmente previsível.

Resumidamente, pode-se dizer que tudo se passa de forma que quanto mais precisamente se medir uma grandeza, forçosamente mais será imprecisa a medida da grandeza correspondente, chamada de canonicamente conjugada.

O papel do princípio da incerteza nas formulações modernas da mecânica quântica

Hoje em dia, o princípio da incerteza é importante principalmente por dois motivos: um histórico e outro didático. Ambos são análogos: o princípio da incerteza mostra de maneira clara que concepções clássicas a respeito da medida devem ser abandonadas.

No entanto, o princípio da incerteza *não* é um bom princípio (ou postulado) da mecânica quântica, já que é inexato e pouco geral. A mecânica quântica não-relativística é totalmente descrita com alguns postulados, dos quais as relações de incerteza de Heisenberg surgem de forma pouco natural. Mas o espírito do princípio da incerteza é mantido: não se pode ter um sistema que, ao ser medido, tenha a probabilidade 1 de se encontrar tanto uma ou outra grandeza, se essas grandezas corresponderem a operadores que não comutam. Iremos explicar isto melhor adiante:

Todas as grandezas que podem ser medidas correspondem aos chamados "autovalores" de certos objetos matemáticos chamados de operadores (na verdade, a natureza requer que esses operadores sejam de uma classe especial, a dos "observáveis"). Chamemos um operador qualquer de A, e chamemos seus autovalores de a_n (a_1 é um autovalor, a_2 é outro e assim por diante). Existem estados quânticos, chamados "autoestados" (que representaremos por $|\phi _{n}>$ ) do operador A, nos quais uma medida tem 100% de chance de encontrar o valor a_n. Esses autoestados e esses autovalores são definidos pela seguinte equação:

$equação Graceli estatística tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

$A|\phi _{n}>=a_{n}|\phi _{n}>$

Um operador é dito um observável se esses autoestados $\phi _{n}>$ formarem uma "base". Diz-se que um grupo qualquer de estados quânticos formam uma base se qualquer outro estado quântico puder ser escrito como uma superposição deles. Ou seja, para qualquer estado quântico $|\Psi >$ ,

$|\Psi >=\sum c_{n}|\phi _{n}>$

Onde os coeficientes $c_{n}$ , em geral complexos, indicam o quanto os autoestados correspondentes $|\phi _{n}>$ influenciam no estado resultante, $|\Psi >$ . Um dos postulados da mecânica quântica diz que a probabilidade de uma medida da grandeza A revelar o valor a_n é:

$equação Graceli estatística tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

$P(a_{n})=|c_{n}|^{2}$

Quando o sistema está no autoestado $|\phi _{n}>$ , o postulado acima mostra que a probabilidade de se encontrar o valor a_n correspondente é 100%. Assim, pode-se dizer que o sistema *possui a grandeza A bem definida*.

Agora consideremos dois operadores A e B, como o operador da posição e o operador do momento. Em geral, os autoestados de um operador não são os mesmos autoestados do outro operador. Consequentemente, se o sistema está em um estado quântico onde a grandeza A é bem definida, a grandeza B não será bem definida. Ou seja, haverá uma "incerteza" na grandeza B.

Mas, e se o sistema estiver em um estado onde a grandeza A é bem definida, e efetuarmos uma medida na grandeza B? Pode-se pensar que, então, saberemos exatamente o valor de ambas as grandezas. Mas isso está errado, devido a outro dos postulados da mecânica quântica: se uma medida de uma grandeza qualquer B revela o valor b_n, então o sistema *é perturbado pela medida*, e passa para o autoestado $|\phi _{n}>$ correspondente à grandeza A_n.

Então, suponha que dois operadores A e B não possuem os mesmos autoestados. Se efetuarmos em um sistema qualquer a medida da grandeza A, e encontrarmos um certo valor, o sistema se torna um autoestado de A, com um valor bem definido de A e uma incerteza no valor de B. Se, após isso, efetuarmos uma medida no valor de B, então lançamos o sistema em um autoestado de B, com um valor bem definido de B e uma incerteza no valor de A. Com isso, dizemos que é impossível saber simultaneamente o valor da grandeza A e da grandeza B.

A incerteza entre a posição e o momento proposta por Heisenberg é, então, uma consequência dos postulados da mecânica quântica, e não um postulado por si só.

Quebra espontânea de simetria é um processo pelo qual um sistema simétrico passa, de forma espontânea, para um estado não simétrico. Este tipo de processo, incomum na natureza física, é vital para a compreensão do modelo padrão das partículas fundamentais, que é um dos mais importantes ramos da física moderna.

Definição

Para que uma quebra espontânea de simetria ocorra, deve necessariamente haver um sistema no qual existam diversos estados subsequentes com iguais probabilidades de ocorrer. Este sistema, como um todo, então é tratado como um sistema simétrico. Entretanto apenas um dos estados subsequentes deve ocorrer e toda a probabilidade dos inúmeros estados diversos é reduzida a zero, já que não há mais simetria. Então, é dito que a simetria do sistema foi espontaneamente quebrada.

Definição formal

Quando uma teoria é dita simétrica com respeito à um grupo simétrico, mas afirma que um elemento deste grupo é distinto, então uma quebra espontânea de simetria ocorreu, ou seja, pela teoria, não é necessário que se identifique o elemento e sim apenas que haja um elemento distinto.

Importância no modelo padrão

Ver artigo principal: Mecanismo de Higgs

Sem a quebra espontânea de simetria o modelo padrão prediz a existência de um determinado número de partículas. Entretanto, algumas destas partículas (os bosões W e Z, por exemplo) são preditos de não possuir massa, quando na realidade eles possuem massa. Esta era a maior falha do modelo até que o físico escocês Peter Higgs e outros propuseram, através do que ficou conhecido por mecanismo de Higgs, o uso da quebra espontânea de simetria para comportar massa nestas partículas. O mecanismo por sua vez prediz a existência de uma nova partícula, o bosão de Higgs. O bosão/bóson de Higgs foi detectado no LHC do CERN em Julho de 2012, com probabilidade maior que 5 sigmas de ser verdadeira tal identificação.

Uso na matemática

Gráfico conhecido por função potencial do chapéu mexicano.

Na matemática o uso mais comum da quebra espontânea de simetria é pelo uso da Função de Lagrange, a qual essencialmente indica como um sistema irá se comportar por meio de termos potenciais

$equação Graceli estatística tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

(1)\qquad {\mathcal {L}}=\partial ^{\mu }\phi \partial _{\mu }\phi -V(\phi ).

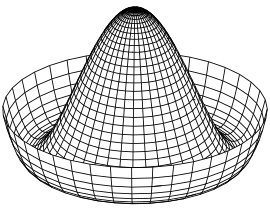
É neste termo potencial $V(\phi )$ que a ação da quebra de simetria ocorre. Como demonstra o gráfico do chapéu mexicano

$equação Graceli estatística tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

(2)\qquad V(\phi )=-10|\phi |^{2}+|\phi |^{4}\,

Este termo potencial possui vários possíveis mínimos dados por

$equação Graceli estatística tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

(3)\qquad \phi ={\sqrt {5}}e^{i\theta }

para qualquer real no intervalo $0<\theta <2\pi$ . Este sistema também possui um estado do vácuo quântico que corresponde ao $\phi =0$ , este estado possui um grupo unitário simétrico. Entretanto, uma vez que o sistema atinja um estado específico no vácuo (que corresponda a um valor para $\theta$ ) a simetria será espontaneamente quebrada.

Em física, um modelo sigma é um sistema físico^[1] que é descrito por uma densidade de Lagrange da forma:

$equação Graceli estatística tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

{\mathcal {L}}(\phi _{1},\phi _{2},\ldots ,\phi _{n})=\sum _{i=1}^{n}\sum _{j=1}^{n}g_{ij}\;\mathrm {d} \phi _{i}\wedge {*\mathrm {d} \phi _{j}}

Pesquisar este blog

MECÂNICA GRACELI - QUÂNTICA TENSORIAL DE CAMPOS [595]

O papel do princípio da incerteza nas formulações modernas da mecânica quântica

Definição

Definição formal

Importância no modelo padrão

Uso na matemática

Comentários

Postar um comentário